介绍 || 张量 || 自动求导 || 构建模型 || TensorBoard支持 || 训练模型 || 模型理解

自动求导的基础知识

Created On: Nov 30, 2021 | Last Updated: Feb 26, 2024 | Last Verified: Nov 05, 2024

请观看下面的视频或在 YouTube 上观看。

PyTorch的 自动求导 功能是使PyTorch在构建机器学习项目时灵活且快速的原因之一。它允许对复杂计算进行快速且简单的多重偏导数（也称为 梯度）计算。这一操作对于基于反向传播的神经网络学习至关重要。

自动求导的强大之处在于它在运行时动态记录计算，这意味着如果您的模型包含决策分支或者长度在运行时才能确定的循环，计算仍会被正确地记录，您将获得能够驱动学习的正确梯度。这一特性，加上模型使用Python构建，比依赖静态分析的更加僵化的框架提供了更大的灵活性。

我们为什么需要自动求导？

机器学习模型是一个 函数，具有输入和输出。在本次讨论中，我们将输入视为一个 i-维向量 \(\vec{x}\)，元素为 \(x_{i}\)。然后我们可以将模型 M 表示为输入的向量值函数：\(\vec{y} = \vec{M}(\vec{x})\)。（我们将M的输出值视为一个向量，因为一般情况下，模型可能有任意数量的输出。）

由于我们主要是在训练上下文中讨论自动求导，因此我们感兴趣的输出将是模型的损失。损失函数 L(\(\vec{y}\)) = L(\(\vec{M}\)(\(\vec{x}\))) 是模型输出的单值标量函数。该函数表明我们模型的预测与某个输入的 理想 输出之间的误差距离。注意：之后在上下文清晰的情况下，我们将省略向量符号，例如使用 \(y\) 代替 \(\vec y\)。

在训练模型时，我们希望最小化损失。在理想情况下，对于一个完美模型，这意味着调整它的学习权重 - 即函数的可调参数 - 使得所有输入的损失为零。在现实情况下，这意味着一种迭代的过程，通过不断调整学习权重，直到在各种输入上得到可接受的损失。

我们如何决定用多大幅度以及向哪个方向调整权重呢？我们想要 最小化 损失，这意味着使它相对于输入的一阶导数等于零：\(\frac{\partial L}{\partial x} = 0\)。

然而，请记住，损失并不是 直接 从输入导出的，而是模型输出的函数（直接是输入的函数），\(\frac{\partial L}{\partial x}\) = \(\frac{\partial {L({\vec y})}}{\partial x}\)。通过微积分中的链式法则，我们得到 \(\frac{\partial {L({\vec y})}}{\partial x}\) = \(\frac{\partial L}{\partial y}\frac{\partial y}{\partial x}\) = \(\frac{\partial L}{\partial y}\frac{\partial M(x)}{\partial x}\)。

\(\frac{\partial M(x)}{\partial x}\) 是复杂的地方。模型输出相对于输入的偏导数，如果我们再次应用链式法则展开表达式，将涉及模型中每个乘法学习权重、每个激活函数以及其他每个数学变换的局部偏导数。每个这样的偏导数的完整表达式是通过计算图中每条可能路径的局部梯度之积的总和，该路径最终以我们试图测量梯度的变量结束。

特别是，学习权重上的梯度对我们很重要 - 它们告诉我们把每个权重调整到哪个方向，以使损失函数更接近零。

因为这样的局部导数的数量（每个都对应模型计算图中的不同路径）通常会随着神经网络的深度指数增加，计算它们的复杂性也如此。这就是自动求导的作用：它跟踪每次计算的历史。PyTorch模型中每个计算的张量都会携带输入张量的历史以及用于创建它的函数的记录。加上PyTorch中的用于执行张量操作的函数都内置了计算其自身导数的实现，这极大地加速了学习所需局部导数的计算。

简单示例

理论讲了很多 - 实际使用自动求导是什么样子的呢？

让我们从一个简单的示例开始。首先，我们导入一些库以便绘制结果：

# %matplotlib inline

import torch

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import math

接下来，我们创建一个充满区间 \([0, 2{\pi}]\) 内均匀间隔值的输入张量，并指定 requires_grad=True。（像其他许多创建张量的函数一样，torch.linspace() 接受一个可选 requires_grad 参数。）设置此标志意味着在后续计算中，自动求导将积累计算的历史记录到输出张量中。

a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
print(a)

tensor([0.0000, 0.2618, 0.5236, 0.7854, 1.0472, 1.3090, 1.5708, 1.8326, 2.0944,
        2.3562, 2.6180, 2.8798, 3.1416, 3.4034, 3.6652, 3.9270, 4.1888, 4.4506,
        4.7124, 4.9742, 5.2360, 5.4978, 5.7596, 6.0214, 6.2832],
       requires_grad=True)

接下来，我们进行一些计算，并在输入与输出上绘制其关系：

b = torch.sin(a)
plt.plot(a.detach(), b.detach())

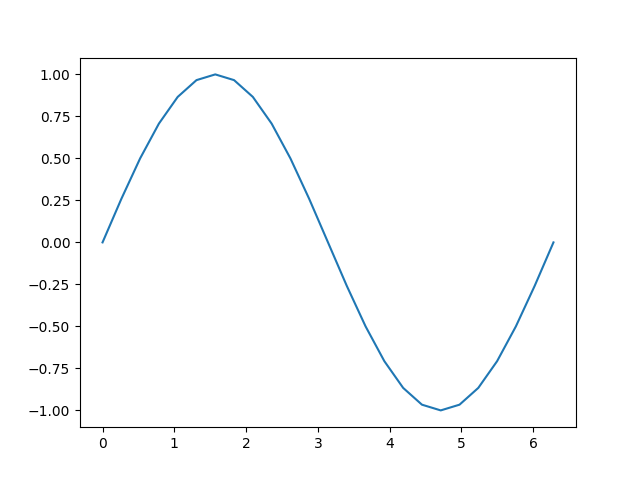
[<matplotlib.lines.Line2D object at 0x7f056779f3d0>]

让我们仔细看看张量 b。当我们打印它时，可以看到它正在跟踪其计算历史的指示符：

print(b)

tensor([ 0.0000e+00,  2.5882e-01,  5.0000e-01,  7.0711e-01,  8.6603e-01,
         9.6593e-01,  1.0000e+00,  9.6593e-01,  8.6603e-01,  7.0711e-01,
         5.0000e-01,  2.5882e-01, -8.7423e-08, -2.5882e-01, -5.0000e-01,
        -7.0711e-01, -8.6603e-01, -9.6593e-01, -1.0000e+00, -9.6593e-01,
        -8.6603e-01, -7.0711e-01, -5.0000e-01, -2.5882e-01,  1.7485e-07],
       grad_fn=<SinBackward0>)

这个 grad_fn 提示我们，当我们执行反向传播步骤并计算梯度时，我们需要计算 \(\sin(x)\) 对此张量所有输入的导数。

让我们进行更多计算：

c = 2 * b
print(c)

d = c + 1
print(d)

tensor([ 0.0000e+00,  5.1764e-01,  1.0000e+00,  1.4142e+00,  1.7321e+00,
         1.9319e+00,  2.0000e+00,  1.9319e+00,  1.7321e+00,  1.4142e+00,
         1.0000e+00,  5.1764e-01, -1.7485e-07, -5.1764e-01, -1.0000e+00,
        -1.4142e+00, -1.7321e+00, -1.9319e+00, -2.0000e+00, -1.9319e+00,
        -1.7321e+00, -1.4142e+00, -1.0000e+00, -5.1764e-01,  3.4969e-07],
       grad_fn=<MulBackward0>)
tensor([ 1.0000e+00,  1.5176e+00,  2.0000e+00,  2.4142e+00,  2.7321e+00,
         2.9319e+00,  3.0000e+00,  2.9319e+00,  2.7321e+00,  2.4142e+00,
         2.0000e+00,  1.5176e+00,  1.0000e+00,  4.8236e-01, -3.5763e-07,
        -4.1421e-01, -7.3205e-01, -9.3185e-01, -1.0000e+00, -9.3185e-01,
        -7.3205e-01, -4.1421e-01,  4.7684e-07,  4.8236e-01,  1.0000e+00],
       grad_fn=<AddBackward0>)

最后，我们计算一个单元素输出。当您调用没有参数的 .backward() 时，该张量必须只包含一个元素，就如我们在计算损失函数时的情况。

out = d.sum()
print(out)

tensor(25., grad_fn=<SumBackward0>)

每个存储在张量中的 grad_fn 都允许您通过其 next_functions 属性回溯到输入。我们可以看到以下对 d 的属性的详细检查显示了所有先前张量的梯度函数。注意 a.grad_fn 显示为 None，表明它是无历史记录输入的函数。

print('d:')
print(d.grad_fn)
print(d.grad_fn.next_functions)
print(d.grad_fn.next_functions[0][0].next_functions)
print(d.grad_fn.next_functions[0][0].next_functions[0][0].next_functions)
print(d.grad_fn.next_functions[0][0].next_functions[0][0].next_functions[0][0].next_functions)
print('\nc:')
print(c.grad_fn)
print('\nb:')
print(b.grad_fn)
print('\na:')
print(a.grad_fn)

d:
<AddBackward0 object at 0x7f062d2c27d0>
((<MulBackward0 object at 0x7f062d2c2800>, 0), (None, 0))
((<SinBackward0 object at 0x7f062d2c2800>, 0), (None, 0))
((<AccumulateGrad object at 0x7f062d2c27d0>, 0),)
()

c:
<MulBackward0 object at 0x7f062d2c2800>

b:
<SinBackward0 object at 0x7f062d2c2800>

a:
None

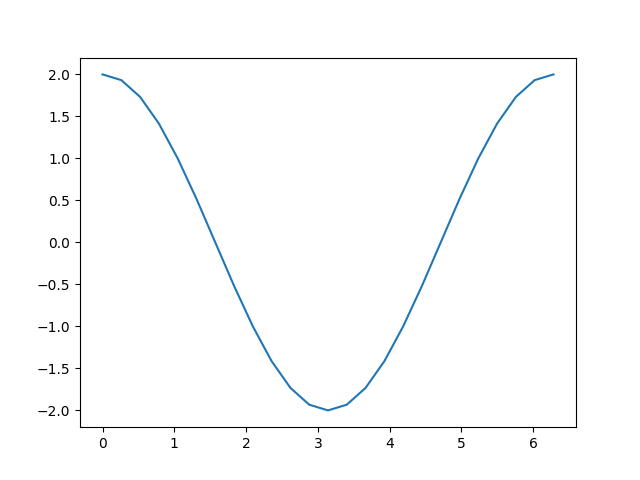
准备好所有这些机制后，我们如何获取导数呢？您可以调用输出上的 backward() 方法，并检查输入的 grad 属性以查看梯度：

out.backward()
print(a.grad)
plt.plot(a.detach(), a.grad.detach())

tensor([ 2.0000e+00,  1.9319e+00,  1.7321e+00,  1.4142e+00,  1.0000e+00,
         5.1764e-01, -8.7423e-08, -5.1764e-01, -1.0000e+00, -1.4142e+00,
        -1.7321e+00, -1.9319e+00, -2.0000e+00, -1.9319e+00, -1.7321e+00,
        -1.4142e+00, -1.0000e+00, -5.1764e-01,  2.3850e-08,  5.1764e-01,
         1.0000e+00,  1.4142e+00,  1.7321e+00,  1.9319e+00,  2.0000e+00])

[<matplotlib.lines.Line2D object at 0x7f062d313b20>]

回想我们所执行的计算步骤：

a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
b = torch.sin(a)
c = 2 * b
d = c + 1
out = d.sum()

添加常数（如我们用于计算``d``的操作）不会改变导数。这就只剩下 \(c = 2 * b = 2 * \sin(a)\)，它的导数应该是 \(2 * \cos(a)\)。观察上图，这恰好是我们所看到的。

请注意只有 计算的叶节点 有梯度被计算。如果您尝试 print(c.grad)，您会得到 None 。在这个简单的示例中，只有输入是叶节点，所以只有它的梯度被计算。

训练中的自动求导

我们简单介绍了自动求导的工作原理，但在其预期目的下，它如何工作呢？让我们定义一个小模型并检查在单个训练批次后它会发生什么变化。首先定义几个常量，我们的模型，以及一些输入和输出的替代值：

BATCH_SIZE = 16
DIM_IN = 1000
HIDDEN_SIZE = 100
DIM_OUT = 10

class TinyModel(torch.nn.Module):

    def __init__(self):
        super(TinyModel, self).__init__()

        self.layer1 = torch.nn.Linear(DIM_IN, HIDDEN_SIZE)
        self.relu = torch.nn.ReLU()
        self.layer2 = torch.nn.Linear(HIDDEN_SIZE, DIM_OUT)

    def forward(self, x):
        x = self.layer1(x)
        x = self.relu(x)
        x = self.layer2(x)
        return x

some_input = torch.randn(BATCH_SIZE, DIM_IN, requires_grad=False)
ideal_output = torch.randn(BATCH_SIZE, DIM_OUT, requires_grad=False)

model = TinyModel()

您可能会注意到，我们从未特意为模型层指定 requires_grad=True。在 torch.nn.Module 的子类中，默认假定我们希望对学习的层权重进行梯度跟踪。

如果我们查看模型的各层，可以检查权重的值，并验证尚未计算梯度：

print(model.layer2.weight[0][0:10]) # just a small slice
print(model.layer2.weight.grad)

tensor([-0.0292, -0.0209, -0.0270,  0.0166,  0.0394, -0.0316, -0.0648,  0.0308,
         0.0562,  0.0476], grad_fn=<SliceBackward0>)
None

让我们看看当我们训练一个批次后会发生什么变化。对于损失函数，我们将简单使用预测和理想输出之间的欧几里得距离的平方，并使用一个基本的随机梯度下降优化器。

optimizer = torch.optim.SGD(model.parameters(), lr=0.001)

prediction = model(some_input)

loss = (ideal_output - prediction).pow(2).sum()
print(loss)

tensor(162.3978, grad_fn=<SumBackward0>)

现在，让我们调用 loss.backward() 并看到会发生什么：

loss.backward()
print(model.layer2.weight[0][0:10])
print(model.layer2.weight.grad[0][0:10])

tensor([-0.0292, -0.0209, -0.0270,  0.0166,  0.0394, -0.0316, -0.0648,  0.0308,
         0.0562,  0.0476], grad_fn=<SliceBackward0>)
tensor([ 4.7434,  5.4197,  0.3396,  0.8107,  1.3478,  4.4255,  1.2944,  0.6542,
        -0.1622,  6.3877])

我们看到每个学习权重都计算出了梯度，但权重保持不变，因为我们还没有运行优化器。优化器负责根据计算出的梯度更新模型权重。

optimizer.step()
print(model.layer2.weight[0][0:10])
print(model.layer2.weight.grad[0][0:10])

tensor([-0.0339, -0.0264, -0.0273,  0.0158,  0.0380, -0.0360, -0.0661,  0.0301,
         0.0563,  0.0412], grad_fn=<SliceBackward0>)
tensor([ 4.7434,  5.4197,  0.3396,  0.8107,  1.3478,  4.4255,  1.2944,  0.6542,
        -0.1622,  6.3877])

您应该看到 layer2 的权重发生了变化。

重要的一点是：调用 optimizer.step() 之后，您需要调用 optimizer.zero_grad()，否则每次您运行 loss.backward() 时，学习权重的梯度都会积累：

print(model.layer2.weight.grad[0][0:10])

for i in range(0, 5):
    prediction = model(some_input)
    loss = (ideal_output - prediction).pow(2).sum()
    loss.backward()

print(model.layer2.weight.grad[0][0:10])

optimizer.zero_grad(set_to_none=False)

print(model.layer2.weight.grad[0][0:10])

tensor([ 4.7434,  5.4197,  0.3396,  0.8107,  1.3478,  4.4255,  1.2944,  0.6542,
        -0.1622,  6.3877])
tensor([19.3569, 28.6464,  5.4837,  8.3619, -2.3330, 21.1472, 17.7357,  2.5104,
        -9.8780, 12.5904])
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

运行上面的代码后，您会看到多次运行 loss.backward() 后，大多数梯度的幅值会变得更大。如果在运行下一训练批次之前没有清零梯度，这些梯度就会因这种现象而爆炸，导致学习结果不正确且不可预测。

打开和关闭自动求导

有些情况下，您需要对是否启用自动求导进行精细控制。根据具体情况，有多种方法可以做到这一点。

最简单的方法是直接修改张量上的 requires_grad 标志：

a = torch.ones(2, 3, requires_grad=True)
print(a)

b1 = 2 * a
print(b1)

a.requires_grad = False
b2 = 2 * a
print(b2)

tensor([[1., 1., 1.],
        [1., 1., 1.]], requires_grad=True)
tensor([[2., 2., 2.],
        [2., 2., 2.]], grad_fn=<MulBackward0>)
tensor([[2., 2., 2.],
        [2., 2., 2.]])

在上面的代码中，我们看到 b1 有一个 grad_fn``（即一个已经跟踪的计算历史），这是预期的，因为它来源于开启自动求导的张量``a。当我们通过 a.requires_grad = False 显式关闭自动求导时，计算历史就不再跟踪了。计算得到的 b2 证实了这一点。

如果您只需要暂时关闭自动求导，最好使用 torch.no_grad()：

a = torch.ones(2, 3, requires_grad=True) * 2
b = torch.ones(2, 3, requires_grad=True) * 3

c1 = a + b
print(c1)

with torch.no_grad():
    c2 = a + b

print(c2)

c3 = a * b
print(c3)

tensor([[5., 5., 5.],
        [5., 5., 5.]], grad_fn=<AddBackward0>)
tensor([[5., 5., 5.],
        [5., 5., 5.]])
tensor([[6., 6., 6.],
        [6., 6., 6.]], grad_fn=<MulBackward0>)

torch.no_grad() 也可以用作函数或方法的装饰器：

def add_tensors1(x, y):
    return x + y

@torch.no_grad()
def add_tensors2(x, y):
    return x + y


a = torch.ones(2, 3, requires_grad=True) * 2
b = torch.ones(2, 3, requires_grad=True) * 3

c1 = add_tensors1(a, b)
print(c1)

c2 = add_tensors2(a, b)
print(c2)

tensor([[5., 5., 5.],
        [5., 5., 5.]], grad_fn=<AddBackward0>)
tensor([[5., 5., 5.],
        [5., 5., 5.]])

有一个对应的上下文管理器 torch.enable_grad()，用于在自动求导未启用时将其打开。它也可以用作装饰器。

最后，可能会有一种情况：一个张量需要跟踪梯度，但你需要一个不跟踪梯度的副本。这时可以使用 Tensor 对象的 detach() 方法——它会创建一个与计算历史 分离 的张量副本：

x = torch.rand(5, requires_grad=True)
y = x.detach()

print(x)
print(y)

tensor([0.7315, 0.7267, 0.6421, 0.9905, 0.1620], requires_grad=True)
tensor([0.7315, 0.7267, 0.6421, 0.9905, 0.1620])

我们之前在绘制某些张量的时候已经用过这种方法。这是因为 matplotlib 需要一个 NumPy 数组作为输入，而从 PyTorch 张量到 NumPy 数组的隐式转换对带有 requires_grad=True 的张量是不可用的。创建一个分离的副本可以让我们继续前进。

自动微分与就地操作

到目前为止，在本笔记本中的每个示例中，我们都使用变量来捕获计算的中间值。自动微分需要这些中间值来执行梯度计算。*因此，使用自动微分时必须谨慎使用就地操作。*进行就地操作可能会破坏调用 backward() 时计算导数所需的信息。如果您尝试对需要自动微分的叶变量进行就地操作，PyTorch 会阻止您，如下所示。

备注

以下代码单元会引发运行时错误。这是预期的行为。

a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
torch.sin_(a)

自动微分性能分析器

自动微分会详细跟踪您计算的每一步。这种计算历史结合时间信息，可用作一个有用的性能分析器——而自动微分内置了这一功能。以下是快速示例：

device = torch.device('cpu')
run_on_gpu = False
if torch.cuda.is_available():
    device = torch.device('cuda')
    run_on_gpu = True

x = torch.randn(2, 3, requires_grad=True)
y = torch.rand(2, 3, requires_grad=True)
z = torch.ones(2, 3, requires_grad=True)

with torch.autograd.profiler.profile(use_cuda=run_on_gpu) as prf:
    for _ in range(1000):
        z = (z / x) * y

print(prf.key_averages().table(sort_by='self_cpu_time_total'))

/data1/lin/pytorch-tutorials/beginner_source/introyt/autogradyt_tutorial.py:485: FutureWarning:

The attribute `use_cuda` will be deprecated soon, please use ``use_device = 'cuda'`` instead.

------------------------------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------
                                Name    Self CPU %      Self CPU   CPU total %     CPU total  CPU time avg     Self CUDA   Self CUDA %    CUDA total  CUDA time avg    # of Calls
------------------------------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------
          cudaGetDeviceProperties_v2        51.30%      14.318ms        51.30%      14.318ms       1.790ms       0.000us         0.00%       0.000us       0.000us             8
                     cudaEventRecord        27.83%       7.767ms        27.83%       7.767ms       1.942us       0.000us         0.00%       0.000us       0.000us          4000
                           aten::div        10.47%       2.923ms        10.47%       2.923ms       2.923us       6.201ms        49.95%       6.201ms       6.201us          1000
                           aten::mul        10.30%       2.875ms        10.30%       2.875ms       2.875us       6.214ms        50.05%       6.214ms       6.214us          1000
               cudaDeviceSynchronize         0.05%      12.974us         0.05%      12.974us      12.974us       0.000us         0.00%       0.000us       0.000us             1
               cudaStreamIsCapturing         0.04%       9.894us         0.04%       9.894us       0.412us       0.000us         0.00%       0.000us       0.000us            24
    cudaDeviceGetStreamPriorityRange         0.01%       2.471us         0.01%       2.471us       2.471us       0.000us         0.00%       0.000us       0.000us             1
                  cudaGetDeviceCount         0.00%       0.364us         0.00%       0.364us       0.182us       0.000us         0.00%       0.000us       0.000us             2
------------------------------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------  ------------
Self CPU time total: 27.909ms
Self CUDA time total: 12.415ms

性能分析器还可以标记代码的单独子块，根据输入张量形状分解数据，并将数据导出为 Chrome 跟踪工具文件。有关 API 的完整详细信息，请参阅 文档。

高级主题：更多自动微分细节和高级API

如果您有一个 n 维输入和 m 维输出的函数 \(\vec{y}=f(\vec{x})\)，完整的梯度是一个输出与每个输入的衍生矩阵，称为 雅可比矩阵：

\[J = \left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\]

如果您有第二个函数 \(l=g\left(\vec{y}\right)\)，它接受 m 维输入（即与上述输出具有相同维数）并返回一个标量输出，您可以将它相对于 \(\vec{y}\) 的梯度表示为列向量 \(v=\left(\begin{array}{ccc}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)^{T}\) - 它实际上是一个单列雅可比矩阵。

更具体地，将第一个函数想象为您的 PyTorch 模型（可能有许多输入和输出），第二个函数为损失函数（模型输出作为输入，损失值作为标量输出）。

如果我们把第一个函数的雅可比矩阵与第二个函数的梯度相乘并应用链式法则，我们得到：

\[J^{T}\cdot v=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{1}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{1}}{\partial x_{n}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\left(\begin{array}{c} \frac{\partial l}{\partial y_{1}}\\ \vdots\\ \frac{\partial l}{\partial y_{m}} \end{array}\right)=\left(\begin{array}{c} \frac{\partial l}{\partial x_{1}}\\ \vdots\\ \frac{\partial l}{\partial x_{n}} \end{array}\right)\]

注意：您也可以使用等效的操作 \(v^{T}\cdot J\)，得到一个行向量。

所得到的列向量是 第二个函数对第一个函数输入的梯度——在我们的模型和损失函数的情况下，就是损失相对于模型输入的梯度。

``torch.autograd`` 是计算这些乘积的引擎。 这就是我们在反向传播过程中积累学习权重上的梯度的方式。

因此，backward() 调用还可以接收一个可选的向量输入。该向量表示张量上的一组梯度，这些梯度会与自动微分跟踪的前一个张量的雅可比矩阵相乘。让我们用一个小向量试试具体的例子：

x = torch.randn(3, requires_grad=True)

y = x * 2
while y.data.norm() < 1000:
    y = y * 2

print(y)

tensor([1284.7465, -329.5719,  899.2652], grad_fn=<MulBackward0>)

如果我们现在尝试调用 y.backward()，会得到一个运行时错误并显示消息，表明仅可为标量输出 隐式地 计算梯度。对于多维输出，自动微分希望我们提供这三个输出的梯度，以便它可以与雅可比矩阵相乘：

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float) # stand-in for gradients
y.backward(v)

print(x.grad)

tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])

（注意，输出梯度都与二次方相关——这是符合重复倍增操作预期的结果。）

高级API

在自动微分上有一个API，它允许您直接访问重要的微分矩阵和向量操作。特别是，它允许您计算特定输入和函数的雅可比矩阵和 *海森矩阵*（海森矩阵类似于雅可比矩阵，但表示所有的二阶导数）。它还提供了与这些矩阵进行向量积的方法。

让我们对一个简单函数计算雅可比矩阵，并使用两个单元素输入进行评估：

def exp_adder(x, y):
    return 2 * x.exp() + 3 * y

inputs = (torch.rand(1), torch.rand(1)) # arguments for the function
print(inputs)
torch.autograd.functional.jacobian(exp_adder, inputs)

(tensor([0.0764]), tensor([0.8322]))

(tensor([[2.1587]]), tensor([[3.]]))

如果仔细看，第一个输出应该等于 \(2e^x\) 的导数是 \(e^x\)），第二个值应该是 3。

当然，您可以对高阶张量执行此操作：

inputs = (torch.rand(3), torch.rand(3)) # arguments for the function
print(inputs)
torch.autograd.functional.jacobian(exp_adder, inputs)

(tensor([0.9696, 0.5702, 0.7823]), tensor([0.1749, 0.4662, 0.1587]))

(tensor([[5.2735, 0.0000, 0.0000],
        [0.0000, 3.5374, 0.0000],
        [0.0000, 0.0000, 4.3731]]), tensor([[3., 0., 0.],
        [0., 3., 0.],
        [0., 0., 3.]]))

torch.autograd.functional.hessian() 方法完全相同（假设您的函数是二次可微的），但会返回所有二阶导数的矩阵。

如果提供一个向量，该函数还可以直接计算向量-雅可比矩阵乘积：

def do_some_doubling(x):
    y = x * 2
    while y.data.norm() < 1000:
        y = y * 2
    return y

inputs = torch.randn(3)
my_gradients = torch.tensor([0.1, 1.0, 0.0001])
torch.autograd.functional.vjp(do_some_doubling, inputs, v=my_gradients)

(tensor([ -99.9576, 1004.6924, 1051.1760]), tensor([5.1200e+01, 5.1200e+02, 5.1200e-02]))

torch.autograd.functional.jvp() 方法执行与 vjp() 相同的矩阵乘法，但操作数是反转的。vhp() 和 hvp() 方法对向量-海森矩阵乘积也有相同作用。

有关详细信息，包括性能注意事项，请参阅 功能API文档。